Многие родители говорят, что успехи их детей связаны с тем, что я хорошо объясняю материал. Так вот, они ошибаются)))))
На самом деле, я почти не ничего объясняю, но структурирую материал так, чтобы ученик мог самостоятельно найти решение незнакомого ему ранее типа задач. Как это происходит, можно посмотреть в представленных ниже видеофрагментах моих уроков.

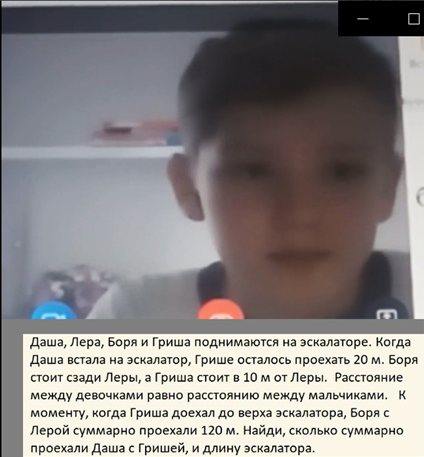Влад М., 4 класс, 10 лет
ССЫЛКА НА ВИДЕО
Олимпиадные задачи. 2022/23 учебный год.
Длительность: 9 минут (в ролике частично сохранено время, когда Влад обдумывает задачу).
С Владом занимались с начала 1-го класса. На видео ниже можно наблюдать этапы роста ученика как математика на протяжении предыдущих двух лет (в 3 и 2 классах). 

Влад М., 3 класс, 9 лет
ССЫЛКА НА ВИДЕО
Олимпиадные задачи. 2021/22 учебный год.
Длительность: 4 минуты.

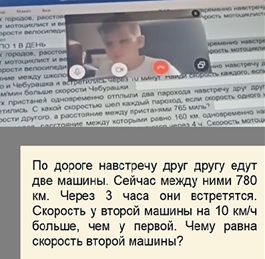Влад М., 2 класс, 8 лет
ССЫЛКА НА ВИДЕО
Задачи на движение. 2020/21 учебный год. 
Длительность: 5 минут.

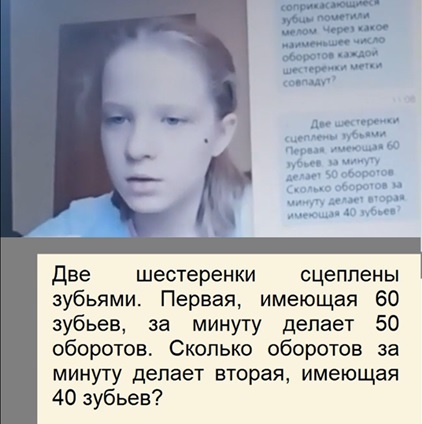Соня Г., 4 класс, 9 лет
ССЫЛКА НА ВИДЕО
Олимпиадные задачи. 2021/22 учебный год.
Длительность: 5 минут.

Вася Г., 3 класс, 9 лет
ССЫЛКА НА ВИДЕО
Олимпиадные задачи. 2021/22 учебный год.
Длительность: 16 минут. В ролике сохранено время, затраченное учеником на обдумывание задачи.

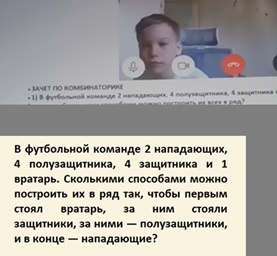Степа М., 4 класс, 11 лет
ССЫЛКА НА ВИДЕО
Урок комбинаторики. 2020/21 учебный год.
Длительность: 14 минут.

Саша Р., дошкольник, 6 лет
ССЫЛКА НА ВИДЕО
Задачи на логику. 2020/21 учебный год.
Длительность: 6 минут.

 На видео показаны именно рабочие моменты моих уроков, т.е. не демонстрация уже пройденных и закрепленных тем, а сам процесс освоения нового материала.
Благодарю родителей моих учеников за помощь в выполнени  видео и  разрешение на их публикацию.

ЗАДАЧИ

ЗДЕСЬ МЫ РАССМОТРИМ, КАК РОДИТЕЛЮ РАБОТАТЬ С РЕБЕНКОМ НАД СЛОЖНЫМИ ЗАДАЧАМИ.

Задача на движение.
Эта задача была предложена когда-то на Курчатовской олимпиаде, теперь периодически «всплывает» на экзаменах (понятно, в разных интерпретациях) и входит в подготовительный курс многих матшкол. Очень красивая задача!
УСЛОВИЕ
Чтобы отвезти мальчика в школу, машина регулярно приезжает в 7 ч 15 мин и доставляет ученика вовремя. Но однажды в 6 ч 50 мин мальчик вышел из дома и пошел в противоположном направлении от школы. Когда приехал водитель в 7 ч 15 мин к дому, то не обнаружил мальчика. Он поехал за ним и, догнав его, привез в школу с десятиминутным опозданием. Во сколько раз скорость мальчика меньше скорости машины?
РЕШЕНИЕ
Эту задачу лучше решать с ребенком в течение нескольких дней, задавая ему вопросы и направляя его мысль в нужном направлении. Диалог обычно складывается примерно так.
РЕБЕНОК:
— …Ну ее же невозможно решить!!!
ВЗРОСЛЫЙ:
— Почему?
— Ну мы же не знаем, какое расстояние он прошел!
— А это обязательно знать? Скажи, если я прохожу от школы до дома за 5 минут, а ты за 10 минут, чья скорость больше и во сколько раз?
— Твоя, в 2 раза.
— А если пешеход идет от города до поселка 1 час, а машина едет 3 минуты, во сколько раз больше ее скорость?
— В 20 раз.
— Теперь читай задачу снова и думай.
В течение дня у ребенка появляются разные идеи, нужно зафиксировать его внимание на правильной, когда он обратит наконец внимание на 10 минут опоздания.
Родитель помогает:
— Подумай, откуда взялись эти 10 минут опоздания? Какой лишний участок пути пришлось проехать машине за эти 10 минут?
Дальше ребенок начинает понимать механику задачи, понимает, что 10 минут — это машина едет от дома до мальчика и потом от места встречи с ним до дома. И все-таки обычно допускает ошибку и не учитывает, что когда машина ехала от дома до мальчика — мальчик в это время тоже шел (т.е. пропускает действие №3 внизу), так что обычно первый (неправильный) ответ — в 5 раз.
— Подумай, сколько времени шел мальчик до встречи с машиной? Нет, не 25 минут. Когда мальчик прошел 25 минут, машина только подъехала к его дому.
…И вот, наконец получаем правильное решение.
1) 7ч 15мин — 6ч 50мин = 25 (мин) — на 25 мин мальчик вышел раньше.
2) 10 : 2 = 5 (мин) — ехала машина от дома мальчика до встречи с ним.
3) 25 + 5= 30 (мин) — шёл мальчик до встречи с машиной.
4) 30:5=6 (раз) — в 6 раз скорость мальчика меньше скорости машины.
Недельки через две-три можно снова дать эту задачу. Даже во второй раз ребенок обычно испытывает сложности при решении, но потом все-таки справляется самостоятельно.

ЗАДАЧИ ГЕОМЕТРИЧЕСКИЕ
Эта задача из вступительной работы по математике в школу №67 (экзамен 2015 года). Подобного типа задачи достаточно часто встречаются на вступительном тестировании в математические школы.
УСЛОВИЕ
К прямоугольнику с двух противоположных сторон приклеили равные квадраты так, что получился новый прямоугольник. Периметр получившегося прямоугольника оказался на 52 см больше периметра первоначального прямоугольника. Найди периметр каждого квадрата и объясни своё решение.
РЕШЕНИЕ
Задача несложная и типичная для вступительной работы. Выполнять ее лучше с рисунком. Нарисовать прямоугольник, пририсовать квадраты с двух сторон. Здесь ребенок может возмутиться:
— Но здесь же не сказано, к какой стороне пририсовывать квадраты, к длине или к ширине прямоугольника.
Предлагаем сделать два рисунка и потом выбрать подходящий (мы, взрослые, такие хитрые! )))
Если решение дается ребенку с трудом, задаем наводящие вопросы.
— На сколько больше получился новый периметр?
— На 52 сантиметра.
— Слушай, а что тут прибавилось? — даем ребенку фломастер и просим обвести ТОЛЬКО ТО, ЧТО ПРИБАВИЛОСЬ.
Здесь ребенок может ошибиться, обвести у каждого квадрата три стороны вместо двух. Тогда делаем новый рисунок и задаем тот же вопрос. При необходимости повторяем (я имею в виду новый рисунок и старый вопрос) до тех пор, пока ребенок САМ не увидит, что эти 52 сантиметра дают 2 стороны каждого квадрата. Две, а не три! Самое сложное для родителя — удержаться, чтобы не подсказать такую очевидную вещь. Не подсказывайте, не намекайте! Чуть раньше или чуть позже ребенок прозреет, увидит, поймет. Не лишайте маленького математика вкуса победы! 
Дальше решается все просто. 
1) Периметр прямоугольника увеличился на 52 сантиметра за счет того, что прибавились четыре отрезка, каждый равный стороне квадрата.

2) 52 : 4 = 13 (см) — одна сторона квадрата
3) 13 х 4 = 52 (см) — периметр квадрата
Теперь предлагаем решить задачку для второго рисунка. Хоть ребенок уже догадался, что получится то же самое, повторить материал никогда не мешает.
Если ребенок поступает в  школу уровня 1329 или  ФМЛ 30, то можно, отработав и закрепив эту тему, предложить ему задачи посложнее, типа:
От большого прямоугольника с двух противоположных сторон отрезали по квадрату так, что получился маленький прямоугольник. Периметр одного квадрата оказался на 12 см меньше периметра большого прямоугольника. Найди периметр маленького прямоугольника и объясни свое решение.
Эта задача достаточно высокого уровня сложности, была на вступительной работе лет 6-7 назад. На экзамене довести решение до конца почти никому из поступающих не хватило времени, поэтому, на всякий случай, рекомендуется отработать этот тип задач заранее.
Задача внизу сочинена Автором сайта для тех, кто уже прошел на курсах или с репетитором задачи на части (мои дети называют такой тип «Прокруст-С»). Решение несложное, главное хорошо прочитать условие и понять, что происходит в задаче.
На противоположных сторонах квадрата построили по маленькому прямоугольнику так, что получился большой прямоугольник. Периметр большого прямоугольника на 24 см и в 3 раза больше периметра квадрата. Найди  сторону квадрата.
—

Подготовка к поступлению в лицей 1533. Подготовка к поступлению в гимназию 1534. Подготовка к поступлению в школу 1329. Подготовка к поступлению в гимназию 1514. Подготовка к поступлению в школу 2007. Подготовка к поступлению в гимназию 1543. Подготовка к поступлению в гимназию 1567. Подготовка к поступлению в лицей 1568. Подготовка к поступлению в лицей 1580 при МГТУ имени Баумана. Подготовка к математическим олимпиадам. Математические олимпиады для начальной школы. Олимпиада малый мехмат. Репетитор по подготовке к олимпиадам. Репетитор олимпиадной математики.