ВСТУПИТЕЛЬНЫЕ ЭКЗАМЕНЫ В КУРЧАТОВСКУЮ ШКОЛУ И КРИТЕРИИ ОЦЕНКИ РАБОТ

Поступление происходит через олимпиаду по математике, которая проводится в апреле. До 2020 г. в экзамен была включена также творческая работа по русскому языку (написание эссе). В настоящее время экзамен по русскому языку достаточно формален. При выполнении олимпиады по математике необходимо серьезно отнестись к оформлению решения, т.к. малейшая небрежность или потеря этапа решения срезает баллы за задачу по крайней мере наполовину (см. «Критерии оценки», файл внизу страницы).
Ниже представлены образцы вступительных работ в Курчатовскую школу — олимпиад по математике  за 2009, 2016 и 2021 гг. и экзамена по русскому языку за 2016 год. Представлены также «Критерии оценивания задания».
Олимпиадные задачи курчатовской олимпиады как первого, так и второго тура обычно типовые,  среднего и средне-высокого уровня сложности. Начинать готовиться к поступлению (например, посещать сильный математический кружок) желательно года за три до экзамена, т.к. для умения работать с олимпиадными задачами важно не только наличие способностей, но и опыт решения подобных задач. 

Образец экзаменационной работы по математике в  Курчатовскую школу за 2009 год. Моим ученикам: ОТВЕТЫ (ЭР-КУРЧ/2009/С).

Курчатовская олимпиада за 2016 год. Ответы (ЭР-КУРЧ/2016/С).

Курчатовская олимпиада за 2021 год. Ответы (ЭР-КУРЧ/2021/С).

Экзамен по русскому языку в  Курчатовскую школу.

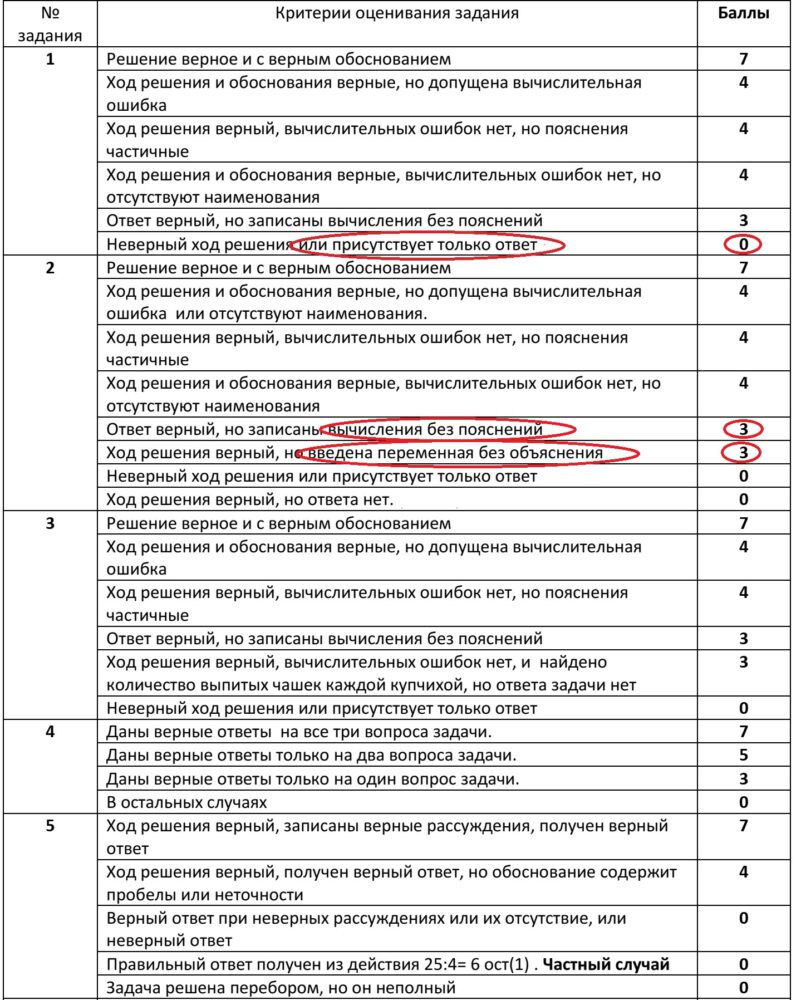
Критерии оценки задач вступительной олимпиады по математике в  Курчатовскую школу (наиболее типичные ошибки при оформления решения выделены красным).