Ниже представлены экзамен в школу 57 по математике в 5 класс за 2015 год, аналог вступительной работы в первый класс по математике (2018/19 учебный год) и образец Открытой устной олимпиады пятьдесят седьмой школы, 6 класс, 1 и 2 туры.
Сильнейшая школа, спецклассы которой из года в год «поставляют» победителей для математических олимпиад самого высокого уровня.
Пятые классы пятьдесят седьмая школа стала набирать недаво. Раньше набирался первый класс и спецклассы средней школы (о системе преподавания в матклассах 57 школы — ЗДЕСЬ).
В настоящее время 57 школа стала набирать и 5 класс. Экзамен по математике состоит из двух туров — письменного и устного, кто сдает хорошо, приглашается на вступительную работу по русскому языку.
Полезно для поступления поучаствовать в Открытой олимпиаде 57 школы «57 задач для младших школьников» для 4 классов, ее результаты учитываются при поступлении.
Экзамен по математике в 5 класс школы № 57 за 2015 год.
Моим ученикам: ОТВЕТЫ (ЭР-57/2015/Е).
Примерный аналог вступительной работы по математике в первый класс 57 школы.
Первый тур Открытой устной олимпиады 57 школы, 6 класс.
Задача 1. Можно ли раскрасить все клетки квадрата размером 4 на 4 в синий и красный цвет, чтобы у каждой красной клетки красных соседей (по стороне) было меньше, чем синих, а у каждой синей — поровну?
Задача 2. Решите’ ребус: fly+fly+fly = аway. Разные буквы обозначают разные цифры, отличные от 0.
Задача 3. Сколько существует способов сложить такого робота, как на рисунке 1, прямоугольниками размера 2×1? (Прямоугольники нельзя накладывать друг на друга, каждая клеточка должна быть закрыта каким-нибудь прямоугольником)
Задача 4. Каждую неделю Робин-Бобин съедает одинаковое число обедов. Робин- Бобин пять дней недели съедает по одному обеду, во вторник два обеда, а ещё в один день недели больше двух обедов. Известно, что за декабрь и январь Робин-Бобин съел 103 обеда. Сколько обедов он съел 1-го февраля?
Задача 5. Папа Карло вырезал из прямоугольника 4×8 два кусочка. Первый является четвертью окружности с центром А и радиусом 4, а второй отрезан по границе круга с центром О — серединой стороны, и радиусом 4 (см. рисунок 2). Кусочек какой площади остался у папы Карло?
Задача 6. а) Вася загадал последовательность из 4 цифр, каждая цифра — 0 или 1. Петя узнал, что загаданная последовательность с последовательностью 1110 имеет 1 общий символ, с последовательностями 0111 и 1101 по три общих символа. Помогите Пете восстановить, какую именно последовательность загадал Вася?
6) Верно ли, что какую бы последовательность ни загадал Вася, Петя всегда сможет разгадать ее, зная только общее число цифр с последовательностями 1110, 0111 и 1101?
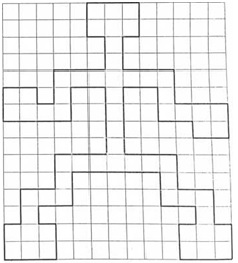Рис. 1 
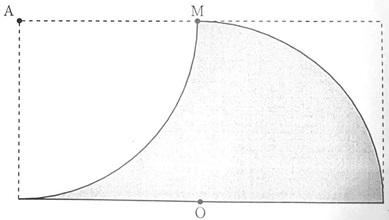Рис. 2
Второй тур Открытой устной олимпиады 57 школы, 6 класс.
Задача 7. Преподаватель летнего математического лагеря взял с собой на все лето несколько рубашек, несколько пар брюк, несколько пар обуви и несколько пиджаков. На каждой лекции он был в брюках, рубашке и обуви, а пиджак надевал не всегда. На любых двух лекциях хотя бы один из элементов его одежды или обуви отличался. Известно, что если бы он взял на одну рубашку больше, то смог бы прочесть на 18 лекций больше; если бы взял на одну пару брюк больше, то смог бы прочесть на 63 лекции больше; если бы взял на одну пару обуви больше, то смог бы прочесть на 42 лекции больше. Сколько пиджаков, рубашек, брюк и пар обуви взял с собой на лето преподаватель?
Задача 8. Внутри шляпы волшебника живут 100 кроликов: белые, синие и зелёные. Известно, что если произвольным образом вытащить из шляпы 81 кролика, то среди них обязательно найдутся три разноцветных. Какое наименьшее количество кроликов нужно достать из шляпы, чтобы среди них точно было два разноцветных?
Задача 9. Имеется 6 шаров, среди которых три радиоактивных, и три детектора, в каждый из которых можно вложить три шара, после чего детектор укажет, есть ли среди них радиоактивный. Известно, что один из детекторов всегда дает верные показания, второй — всегда неправильные, а третий — как повезет. Возможно ли определить, какие из шаров радиоактивные?